پارادکس زنون

آنچه گذشت

مسأله‌ای که در داستان بالا بهنام به آن اشاره ‌کرده است، در حقیقت صورت تغییر یافته‌ای از یک پارادکس مشهور ریاضی است. این پارادکس منسوب به یکی از فلاسفه‌ی قبل از میلاد مسیح (ع)، به نام زنون¹ است. وی در حدود پنج قرن قبل از میلاد در الیا (شهری در جنوب ایتالیای کنونی) می‌زیست. زنون از شاگردان مکتب پارمنیدس² الیایی است و به پیروی از وی معتقد است که در جهان اطراف ما هیچ حرکتی صورت نمی‌گیرد؛ وی در اثبات این ادعا چند پارادکس مطرح می‌کند تا نشان دهد که اگر چه شهود ما چنین حکم می‌کند که اشیاء جهان اطراف می‌توانند حرکت کنند، اما این شهود با مبانی عقلی ما در تناقض است و در حقیقت حرکت نوعی توهم است!

یکی از این پارادکس‌ها به دیکوتومی³ شهرت یافته است. گفته‌های بهنام در داستان بالا در حقیقت برداشتی آزاد از همین پارادکس و برای فریب دادن پرتابه بوده است. صورت اصلی این پارادکس چنین است:

فرض کنید که شخصی بخواهد از نقطه‌ی A به نقطه‌ی B برود (برای سادگی فرض کنید که حرکت بر روی خط مستقیمی که از دو نقطه‌ی A و B می گذرد، انجام می‌شود). برای نیل به این هدف وی ناچار است که ابتدا 2/1 راه را طی کند. هنگامی که شخص این 2/1 ابتدایی راه را طی کرد، 2/1 دیگر راه باقی می‌ماند که باید آن را طی نماید. برای پیمودن این مسیر (باقی مانده) وی باید ابتدا 2/1 آن را طی نماید (در حقیقت 4/1 کل مسیر)، پس تا به این‌جا 4/3 (4/1 + 2/1) کل مسیر طی شده است و 4/1 کل مسیر باقی مانده است. برای پیمودن مسیر باقی مانده وی ابتدا باید نصف آن (یعنی 8/1 کل مسیر) را طی نماید. پس تا به این جای کار، وی 8/7 (8/1 + 4/1 + 2/1) کل مسیر را طی کرده است و 8/1 از آن باقی مانده است. برای طی 8/1 باقی مانده وی ناچار است که ابتدا نصف آن (یعنی 16/1 کل مسیر را طی نماید) و به همین ترتیب این کار را در مراحل بعدی ادامه دهد.

در حقیقت در هر مرحله شخص نصف مسیر باقی مانده تا نقطه‌ی B را طی می‌نماید. حال فرض کنید که وی در m مرحله اقدام به پیمودن فاصله‌ی بین A و B (به روش بیان شده) کرده باشد. از آن ‌جایی که در مرحله‌ی m ام، این فرد m_2/1کل مسیر را طی می‌نماید، پس در پایان مرحله‌ی m ام، به اندازه‌ی  کل مسیر، از نقطه ی B فاصله خواهد داشت. زیرا:

 = (+...+ +  + ) - 

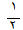پس در حقیقت این فرد بعد از طی هر تعداد متناهی مرحله، باز هم در فاصله‌ای از نقطه‌ی B قرار خواهد داشت؛ و به ناچار این فرد برای رسیدن از A به B، باید تعداد نامتناهی مرحله را پشت سر بگذارد. با استناد به این مسئله، زنون چنین استدلال می‌کند که:

چون گذراندن تعدادی نامتناهی مرحله، در زمانی متناهی ممکن نیست، پس این فرد هیچ ‌گاه نخواهد توانست که از A به B برسد.

دقت کنید که اگر استدلال زنون درست باشد، می‌توان چنین نتیجه گرفت که اساساً هیچ حرکتی ممکن نیست. چرا که می‌توانیم استدلال بالا را عیناً در مورد هر حرکتی معتبر بدانیم.

آیا به راستی حرکت یک توهم است؟

باید گفت که زنون اشتباه بزرگی را مرتکب شده است. وی گمان می‌کرد که جمع هر تعداد نامتناهی از اعداد مثبت یک مقدار نامتناهی است! و بر همین اساس معتقد بود که برای انجام هر کدام از این تعداد نامتاهی مرحله، زمانی لازم است و جمع این مقادیر (که در حقیقت جمع تعدادی نامتناهی از اعداد مثبت است)، نامتناهی است، پس طی کردن همه‌ی این مراحل و در نتیجه رسیدن از A به B ممکن نخواهد بود! اما باید گفت که:

جمع هر تعداد نامتناهی از اعداد مثبت، لزوماً یک مقدار نامتناهی نیست!

این مطلب را امروزه‌ تمام دانش آموزان سال ‌های سوم دبیرستان و پیش‌دانشگاهی به خوبی می دانند! و احتمالاً پرتابه هنوز به سوم دبیرستان نرسیده است که این چنین فریب بهنام را خورد!

2. Parmenides

3. دیکوتومی (Dichotomy) یعنی «تقسیم به "دو" بخش». وجه تسمیه‌ی این پارادکس این است که در آن با تقسیمات متوالی یک مسافت ثابت به "دو"، سر و کار داریم.

نویسنده: صالح زارع پور