فراکتال چیست؟
ما فراکتالها را در زندگی روزمره ی خود به فراوانی مشاهده می کنیم: درخت ها، کوه ها، پراکنده شدن برگ های پاییزی روی زمین. به این تصویرها که در صفحه ی گالری قابل مشاهده است، نگاه کنید و سعی کنید شباهت بین آن ها را درک کنید. حال به این تعریف دقت کنید: فراکتال شکل هندسی چند جزئی است که میتوان آن را به قسمت هایی تقسیم کرد، به طوری که هر قسمت یک کپی از " کل " شکل باشد. حال دوباره به تصویرها نگاه کنید! به سختی می توان باور کرد که چیزی مانند فراکتالها در عین پیچیدگی و کاربرد در عالی ترین سطوح ریاضی، بتواند به شکل یک سرگرمی جالب مورد استفاده قرار گیرد. در واقع هندسه ی فراکتالی، حرکت اشکال در فضا را ثبت میکند و ناهمواری دنیا و انرژی و تغییرات دینامیک آن را نشان میدهد! اما حقیقت این است که فراکتال موضوع ساده ای است. به سادگی ابرها یا شعله های آتش. واژه ی فراکتال از ریشه ای یونانی به معنای " تکه تکه شده " و"بخش بخش" آمده است و به نحوی تعریف ریاضی اش را در خود دارد. به زبان ساده ، اشکال فراکتالی دارای 3 خاصیت عمومی هستند:
• تشابه به خود
• تشکیل از راه تکرار
• بعد کسری
تشابه به خود self similarity
گربهها ، قناریها و کانگوروها به نحوی به هم شبیه هستند. اما در هندسه، تشابه معنای خاصی دارد که حتماً آن را در کتاب ریاضی خود دیده اید و میدانید که تشابه، یکسانی اشکال در عین متفاوت بودن اندازه هاست. به زبان ساده تر اگر بتوانید با بزرگ یا کوچک کردن دو شکل، آن ها را دقیقاً همانند هم کنید، آن دو شکل متشابه اند. اما شکل های خود متشابه کدامها هستند؟ اشکال زیادی وجود دارند که فراکتالی نیستند اما خود متشابه اند.
به این شکل دقت کنید! 
شکل کلی یک ذوزنقه است و خود از ذوزنقه های کوچک تر کنار هم پدید آمده است. این مورد یک مثال از تشابه به خود است.
حال به این مثلث خاص نگاه کنید.

این مثلث بزرگ که مثلث سیرپینسکی نام دارد، از مثلث های مشابه کوچک تر تشکیل شده است که همین طور کوچک تر و کوچک تر هم میشوند.
چند سایز مثلث وجود دارد و آیا همه باهم و با مثلث بزرگ تشابه دارند؟
چند سؤال:
 اگر شکل قرمز را شکل پایه در نظر بگیریم ، در شکل آبی چند نمونه از آن وجود دارد؟
اگر شکل قرمز را شکل پایه در نظر بگیریم ، در شکل آبی چند نمونه از آن وجود دارد؟

 آیا مربعها خود متشابه اند؟ یعنی میتوان با مربع های کوچک تر، مربع بزرگی ساخت. شش ضلعیها چه طور؟
آیا مربعها خود متشابه اند؟ یعنی میتوان با مربع های کوچک تر، مربع بزرگی ساخت. شش ضلعیها چه طور؟
 آیا همه ی دایرهها متشابه اند؟ آیا خود متشابه هم هستند؟
آیا همه ی دایرهها متشابه اند؟ آیا خود متشابه هم هستند؟
تشکیل از راه تکرار Iterative formation
مقصود از تشکیل از راه تکرار چیست؟ یعنی برای درست کردن یک فراکتال میتوانیم یک شکل معمولی هندسی ( مثلاً یک خط ) را انتخاب کنیم و با آن یک شکل بسازیم. سپس با شکل به دست آمده، شکل پیچیده تری مانند شکل های قبلی بسازیم، و همین طور به این کار ادامه دهیم. اشکال فراکتالی به این طریق به وجود میآیند و برنامه های کامپیوتری متعددی برای ایجاد آن ها نوشته شده است که هر کدام نام و روشی خاص دارند. مثلاً مثلث سیرپنسکی که قبلاً مشاهده کردید و یا :
ابعاد کسری fractional dimension
همان طور که میدانید، یک نقطه بعد ندارد.
یک خط، شکلی یک بعدی است
یک صفحه، دو بعد دارد.
و شکل های حجیم، سه بعد دارند.
اما فراکتالها میتوانند بعد کسری داشته باشند! مثلاً 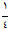 یا
یا 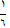 . چه طور چنین چیزی امکان دارد؟
. چه طور چنین چیزی امکان دارد؟
اگر یک پاره خط را نصف کنیم، چه پیش میآید؟
حال دو خط داریم که همانند هم هستند.

اگر هر دو بعد یک مربع را نصف کنیم، چه طور؟ حال چهار مربع هم اندازه داریم.

با نصف کردن هر سه بعد یک مکعب به هشت مکعب کوچک تر میرسیم.

به جدول زیر دقت کنید:
چه الگویی وجود دارد؟ به نظر میرسد که بعد، همان " توان " است. یعنی برای پیدا کردن تعداد اشکال حاصل باید 2 را به توان بعد آن شکل برسانیم. پس میتوانیم مورد زیر را نیز به این جدول اضافه کنیم:
این بار به سراغ مثلث خودمان می رویم. اگر هر ضلع را نصف کنیم، چند مثلث تشکیل میشود؟ به خاطر داشته باشید که مثلث های سفید جزء مثلث سیرپینسکی نیستند. با نصف کردن هر ضلع، به سه مثلث میرسیم، یعنی: 3=2d 3 عددی است بین 21 و22 . کسانی که با لگاریتم آشنایی داشته باشند، به راحتی این مسأله را حل میکنند. برای مطالعه ی بیش تر میتوانید به سایت های زیر مراجعه کنید: http://astronomy.swin.edu.au/~pbourke/fractals/fracintro/ http://www.math.umass.edu/~mconnors/fractal/fractal.html http://www.geom.uiuc.edu/java/ http://mathforum.org/alejandre/workshops/fractal/fractal3.html زیرنویسها 1.self similarity2.iteractive formation 3.fractional dimension | |||||||||||||||||

















