قوانین حرکت در منظومهی شمسی


اولین اقدامات جدی برای توصیف حرکت منظومهی شمسی را یونانیها انجام دادند. بطلمیوس نظریه زمین مرکزی (یا بطلمیوسی) را برای منظومهی شمسی مطرح کرد که در آن، زمین در مرکز منظومه ساکن است و سیارات، از جمله خورشید و ماه، حول آن دوران میکنند.
این مطلب نباید شگفتانگیز جلوه کند زیرا زمین به نظر ما یک جسم بسیار با اهمیت است. حتی امروزه در آموزش اخترشناسی در دریانوردی، از چارچوبِ مرجعِ زمین مرکزی استفاده میکنیم و در مکالمهی معمولی اصطلاحاتی چون «طلوع خورشید» را به کار میبریم که اشاره به چنین چارچوبِ مرجعی است.
مدارهای دایرهای ساده نمیتوانند حرکتهای پیچیدهی سیارات را توجیه کنند، در نتیجه بطلمیوس مفهوم افلاک تدویر را به کار برد. در این مدل هر سیارهای به دور نقطهای در حال دوران است که این نقطه نیز در مداری دایرهای شکل به دور زمین میگردد.
او همچنین مجبور شد به آرایشهای هندسی دیگری هم متوسل شود، اما در هر یک از این افلاک نیز دایره نقش خود را به عنوان شکل اصلی حرکت سیارات حفظ میکرد.
امروزه ما میدانیم که دایره در حرکت سیارات شکل اصلی نیست. بلکه بیضی شکل اصلی حرکت است و خورشید در یکی از کانونهای بیضی قرار دارد.
در قرن شانزدهم میلادی کوپرنیک (1473-1543 میلادی / 852-922 شمسی) یک طرح خورشید مرکزی (کوپرنیکی) پیشنهاد کرد که در آن خورشید در مرکز منظومهی شمسی قرار دارد و زمین مانند یکی از سیاراتش حول آن حرکت میکند. اغلب تصور میشود که طرح کوپرنیک آن چنان سادهتر از طرح بطلمیوس است که باید از همان ابتدا پذیرفته میشد. این تصور درست نیست. کوپرنیک به تقدس دایرههای معتقد بود و او نیز به اندازهی بطلمیوس از افلاک تدویر و طرحهای دیگر استفاده کرد. با این حال قرار دادن خورشید در مرکز اجرام، تعریف بسیار سادهتر و توضیح بسیار طبیعیتر در مورد برخی خصوصیات حرکت سیارهای ارائه داد. مهمتر از همه، او شالودهی محکمی بنیان نهاد که دیدگاههای جدید ما در بارهی منظومهی شمسی بر روی آن استوار است.

بحث و جدل دربارهی این دو نظریه، اخترشناسان را بر آن داشت که اطلاعات رصدی دقیقتری به دست آورند. این اطلاعات را تیکو براهه (1546-1601 میلادی / 925-980 شمسی) آخرین اخترشناس بزرگی که مشاهدات خود را بدون استفاده از تلسکوپ انجام میداد، جمعآوری کرده است.
یوهانی کپلر (1571-1630 میلادی / 950-1009 شمسی) که دستیار براهه بود، مدت بیست سال وقت صرف کرد تا توانست اطلاعات جمعآوری شده توسط براهه را تحلیل و تعبیر کند. کپلر قواعد مهمی برای حرکت سیارات پیدا کرد. این قواعد که به سه قانون کپلر در حرکت سیارات معروفاند عبارتند از :
- تمام سیارات در مدارهای بیضی شکلی که خورشید در یکی از کانونهای آن قرار دارد حرکت میکند. (قانون مدارها)
- خط واصل هر سیاره به خورشید در زمانهای مساوی مساحتهای مساوی جاروب میکند. (قانون مساحتها) به شکل زیر نگاه کنید. هر کدام از این قسمتهای رنگی مساحتی برابر دارند. طبق این قانون سیارهای که به دور خورشید در حال دوران است هر کدام از این قسمتها را در زمانهای مساوی طی میکند.

نیوتون به منظور به دست آوردن سه قانون تجربی کپلر، قوانین حرکت و گرانشاش را با یکدیگر ترکیب کرد : و برای قانون دوم این روابط را برای بدست آوردن سرعت در نقطه اوج و حضیض به دست آورد:

در این رابطه V1 سرعت سیاره است وقتی در نزدیکترین فاصله خود با خورشید قرار دارد (حضیض خورشیدی) که با توجه به این قانون V1 بیشترین سرعتی است که سیاره در حرکت مداری خود خواهد داشت و V2 سرعت سیاره است وقتی که در بیشترین فاصله خود با خورشید قرار دارد. (اوج خورشیدی) A
فاصله متوسط یا همان نیم قطر اطول (بزرگ) مدار سیاره با واحد AU(فاصله متوسط زمین تا خورشید) و P دوره تناوب با واحد سال زمینی و e خروج از مرکز بیضی میباشد.

کپلر برای بدست آوردن این فرمول 7 سال تلاش کرد. در آن زمان فاصله واقعی میان خورشید و سیارات معلوم نبود، اما محاسبه نسبت فاصله یک سیاره تا خورشید به فاصله زمین تا خورشید میسر بود. مثلاً کپلر میدانست که نیم قطر اطول (بزرگ) مدار مریخ تقریباً 5/1 برابر نیم قطر اطول مدار زمین است. حال او متوجه شد اگر در هر سیاره نیم قطر اطول را به توان 3 و دوره گردش (p) را به توان 2 برسانیم. دو رقم بدست آمده باهم برابر میشوند و فقط اختلافهای اندکی برای برجیس (مشتری) و کیوان(زحل) دیده میشود. این مطلب را میتوان به صورت 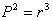 نوشت که درآن p برحسب سال و r برحسب واحد نجومی (نیم قطر اطول زمین) است. میتوانیم برای اندازهگیری دور گردش سیاره واحد روز و برای فاصله کیلومتر را انتخاب کنیم. در این صورت نباید انتظار داشته باشیم
نوشت که درآن p برحسب سال و r برحسب واحد نجومی (نیم قطر اطول زمین) است. میتوانیم برای اندازهگیری دور گردش سیاره واحد روز و برای فاصله کیلومتر را انتخاب کنیم. در این صورت نباید انتظار داشته باشیم  بلکه باید رابطه را به صورت
بلکه باید رابطه را به صورت 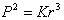 بنوسیم که در آن k ضریب ثابت است و مقدارش به واحدها بستگی دارد. برای مشخص کردن این موضوع معادله را میتوان به این صورت نوشت :
بنوسیم که در آن k ضریب ثابت است و مقدارش به واحدها بستگی دارد. برای مشخص کردن این موضوع معادله را میتوان به این صورت نوشت : 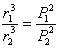
که P1 و r1 برای جرمی است که میخواهیم این مقادیر را برایش بدست آوریم و P2 و r2 معمولاً برای زمین یا جرمی که این دو مقدار برای آن اندازه گیری شده است، میباشد.
قوانین کپلر نظریهی کوپرنیک را قویاً تایید کردند. این قوانین نشان دادند که اگر خورشید به عنوان مرجع در نظر گرفته شود، حرکت سیارات به راحتی قابل توصیف است. اما این قوانین تجربی بودند و صرفاً حرکت مشاهده شدهی سیارات را بدون هیچ گونه تعبیر نظری توصیف میکردند. کپلر تصور نمیکرد که نیرو منشأ این قواعد باشد. در واقع مفهوم نیرو تا آن زمان هنوز فرمولبندی نشده بود. بنابر این، این که نیوتون توانست قوانین کپلر را از قانون حرکت و قانون گرانش خودش نتیجه بگیرد، یک پیروزی بزرگ برای او محسوب میشد. قانون گرانش نیوتن در این مورد ایجاب میکرد که هر سیاره با نیرویی به طرف خورشید جذب شود که با جرم سیاره متناسب است و با مجذور فاصلهی آن از خورشید نسبت معکوس دارد.
نیوتن از این طریق توانست حرکت سیارات در منظومهی شمسی و حرکت اجسام در حال سقوط در نزدیکی سطح زمین را با یک مفهوم واحد بیان کند. بدین ترتیب مکانیک زمینی و مکانیک سماوی را که قبلاً از هم جدا بودند در یک نظریهی واحد با هم تلفیق کرد. اهمیت علمی کار کوپرنیک در این بود که نظریهی خورشید مرکزی راه را برای این تلفیق هموار کرد. در نتیجه، با این فرض که زمین ضمن گردش به دور خود حول خورشید نیز دوران میکند، توجیه پدیدههای متعددی چون حرکت ظاهری روزانه و سالانهی ستارهها، خارج شدن زمین از حالت کروی، رفتار بادهای استوایی و بسیاری چیزهای دیگر که توضیح آنها در نظریهی زمین مرکزی به این راحتی نبود، امکان پذیر شد.
در اینجا آموزنده است که مراحل مختلف شناخت خود از حرکت اجسام در منظومهی شمسی را با توجه به برنامهی مکانیک کلاسیک مرور کنیم. از لحاظ تاریخی چهار تحول بزرگ رخ داده است :
- کوپرنیک خاطر نشان کرد که خورشید در مرکز منظومهی شمسی قرار دارد، نه زمین. به زبان امروزی، او چارچوب مرجعی (خورشید) در اختیار ما قرار داده که از چارچوب مرجعی که قبلاً برای بیان حرکتهای منظومهی شمسی به کار میرفت (زمین) خیلی مناسبتر است. این چارچوب مرجع، که نسبت به خورشید ثابت است و با آن نمیچرخد، اساساً یک چارچوب مرجع لخت است. این از جمله برتریهای سیستم کوپرنیکی است، زیرا چارچوب مرجعی که به زمینِ در حال دوران (که ما بر روی آن زندگی میکنیم) متصل است، نمیتواند برای مسائل مربوط به حرکت سیارات به کار رود.
- براهه حرکت سیارات را آن طور که از زمین دیده میشدند، دقیقاً اندازه گرفت و اطلاعات رصدی لازم را برای پیشرفتهای بعدی فراهم کرد.
- کپلر با مطالعهی دادههای براهه، سه قانون تجربی ساده را که قبلاً به آنها اشاره کردیم، به دست آورد و با قبول چارچوب مرجع کوپرنیکی اطلاعات سینماتیکی مربوط به حرکت سیارات را به شکل سادهای نمایش داد.
- نیوتن صورت کلی قوانین حرکت دستگاههای مکانیکی، از جمله قانون نیروی خاصی که بر حرکت سیارات حاکم است و قانون گرانش جهانی نامیده میشود را کشف کرد.
از این رو، طی قریب 200 سال ما شاهد پیشرفتهای زیر هستیم:
- پیدایش چارچوب مرجع مناسب
- کسب اطلاعات سینماتیکی دقیق
- تعیین قوانین تحربی حرکت سیارات
- کشف قوانین عمومی مکانیک کلاسیک و قانون نیروی مناسب برای حرکت سیارات.
- شبیه سازی قوانین کپلر در منظومه شمسی
اگر مایل هستید که به آزمایش قوانین کپلر بپردازید، میتوانید با کمک شبیهساز زیر سه قانون کپلر را در مورد هر یک از سیارات منظومه شمسی تجربه کنید.
برای این منظور کافی است که در گزینه set parameters for (در قسمت راست صفحه) نام سیارهای که میخواهید به بررسی حرکتش بپردازید را مشخص کنید.
در قسمت planetary orbit simulator میتوانید مدارهای دلخواه خود را رسم کنید و ببینید که سیارهای فرضی در این مدار چگونه به دور خورشید در حال حرکت است. برای این منظور کافی است که گزینههای semimajor axis (AU) (نیم قطر بزرگ با واحد AU) و eccentricity (خروج از مرکز) را به صورت دلخواه خود عدد بدهید تا مداری که میخواهید را داشته باشید. توجه داشته باشید مداری که خروج از مرکز آن 0 باشد دایره است و هر چه خروج از مرکز مداری بیشتر از صفر باشد، بیضیای که خواهیم داشت کشیدهتر خواهد شد. نیم قطر بزرگ، فاصلهی متوسط سیاره تا خورشید است که آن را نیز میتوان به صورت دلخواه خود تعیین کنید.
در قسمت راست صفحه گزینهی دیگر خواهید دید به نام animation rate (yrs/s) که سرعت نمایش حرکت سیاره را نشان میدهد و در واقع از شما میپرسد که میخواهید که حرکتی که اکنون مشاهده میکنید با چه سرعتی برای شما نمایش داده شود. و واحد این سرعت در این برنامه سال به ثانیه میباشد. یعنی هر سال را در چند ثانیه به شما نشان دهد. اگر به طور مثال این گزینه را بر روی عدد 1 قرار دهید به این معناست که هر سال را در یک ثانیه نشان خواهد داد. اگر عدد تعیین شده برای این گزینه از یک کمتر باشد سرعت حرکت سیاره در مدار کمتر خواهد بود و به همین نسبت اگر عدد تعیین شده برای این گزینه بیشتر از یک باشد، سرعت حرکت سیاره در مدار بیشتر خواهد بود.
گزینه start animation در سمت راست صفحه برای شروع شبیهسازی است که با فشار دادن آن سیارهای که شبیهسازی کردید شروع به حرکت در مدار خود میکند و شما میتوانید به بررسی سه قانون کپلر در بارهی آن بپردازید.
در سمت راست صفحه سه گزینهی دیگر نیز وجود دارد که میتوانید آنها را نیز فعال کنید. اولین گزینهی show solar system orbits است که با فعال کردن آن میتوانید مدارهای سیارات نه گانهی منظومهی شمسی به دور خورشید را نیز در تصویر ببینید. گزینهی بعدی show solar system planets میباشد که اگر این گزینه را فعال کنید میتوانید سیارات منظومهی شمسی را در حالی که در مدارهای خود در حال گردش به دور خورشید هستند را مشاهده کنید.
و در آخر، گزینهی سوم label the solar system orbits میباشد که نام هر سیاره را در کنار مدار حرکتش به نمایش در میآورد.
در ابتدا گزینههای دوم و سوم غیرفعال میباشند، برای فعال کردن این دو گزینه ابتدا باید گزینهی یک را انتخاب کنید تا مدار سیارات به دور خورشید نمایش داده شود، سپس به انتخاب گزینهی دوم و سوم بپردازید.
در گوشهی سمت راست پایین نیز کلید clear optional features قرار دارد که با فشار دادن آن این سه گزینه به حالت غیرفعال در میآیند.
بعد از تعیین مدار سیاره و تنظیمات خاص آن بهتر است که در مورد قوانین کپلر تحقیق و آزمایشی داشته باشیم.
در قسمت سمت چپ در پایین صفحه چهار حالت مختلف را برای شما نمایش میدهد. که سه حالت اول مربوط به قوانین سه گانهی کپلر در مورد حرکت سیارات به دور خورشید میباشند و حالت چهارم در مورد سرعت و حرکت سیارات در گردششان به دور خورشید میباشد.
1ـ اگر حالت Kepler`s 1st law را انتخاب کنید، گزینههای مربوط به قانون اول کپلر در اختیار شما قرار داده میشود. این قانون میگوید که : تمام سیارات در مدارهای بیضی شکلی که خورشید در یکی از کانونهای آن قرار دارد حرکت میکند. (قانون مدارها)
همان طور که میدانید در بیضی دو نقطهی ثابت به نام کانونهای بیضی وجود دارد که مجموع فاصلهی هر نقطه بر روی بیضی از این دو نقطه به یک اندازه است.
طبق قانون اول کپلر مدار سیارات در حرکت به دور خورشید به شکل بیضی میباشد که خورشید در یکی از کانونهای این بیضی قرار دارد، خب برای این که کانون دیگر این بیضی را ببینید گزینهی show empty focus را انتخاب کنید تا محل کانون دیگر این بیضی را نیز مشاهده کنید. نقطهی سفید رنگی که در تصویر مشاهده میکنید همان خورشید (یکی از کانونهای بیضی) میباشد. گزینهی show semiminor axis شعاع کوچک بیضی (نیم قطر کوچک بیضی) را نشان میدهد و گزینهی show semimajor axis شعاع بزرگ بیضی را نمایش میدهد. Show center نیز مرکز بیضی را نمایش خواهد داد. در این قسمت در زیر صفحه یک فرمول میبینید که نوشته است 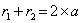 در این فرمول a همان نیم قطر بزرگ بیضی میباشد که تحت عنوان گزینهی semimajor axis در قسمت راست صفحه آن را تعیین کرده بودیم. r1 و r2 به ترتیب فاصلهی سیاره از کانون اول (خورشید) و کانون دوم بیضی میباشد. برای دیدن r1 و r2 بر روی شکل کافی است که گزینهی show radial lines را فعال کنید.
در این فرمول a همان نیم قطر بزرگ بیضی میباشد که تحت عنوان گزینهی semimajor axis در قسمت راست صفحه آن را تعیین کرده بودیم. r1 و r2 به ترتیب فاصلهی سیاره از کانون اول (خورشید) و کانون دوم بیضی میباشد. برای دیدن r1 و r2 بر روی شکل کافی است که گزینهی show radial lines را فعال کنید.
این فرمول همان فرمول شکل بیضی میباشد که برای ما نشان میدهد که مدار سیارات به دور خورشید بیضی شکل میباشند. هر مداری که میخواهید در سمت راست صفحه تعیین و ترسیم کنید ولی باز مشاهده خواهید کرد که مداری که انتخاب کردهاید بیضی شکل میباشد. (این نکته را نباید فراموش کنید که دایره یک نوع خاص بیضی میباشد.) وقتی که سیاره بر روی مدار خود در حال گردش به دور خورشید باشد مقدار r1 و r2 در هر لحظه تغییر میکند ولی بر طبق تعریف بیضی مجموع مقدار r1 و r2 در هر لحظه و برای هر نقطه از بیضی برابر دو برابر نیم قطر بزرگ بیضی میباشد که این موضوع را میتوانید با استفاده از این فرمول در این قسمت مشاهده کنید.
2ـ برای مشاهدهی فرمولهای قانون دوم کپلر کافی است که در سمت چپ و در پایین صفحه حالت Kepler`s 2nd law را انتخاب کنید. در بالا توضیح دادم که قانون دوم کپلر میگوید : خط واصل هر سیاره به خورشید (خطی که سیاره را به خورشید وصل میکند) در زمانهای مساوی مساحتهای مساوی جاروب میکند. (قانون مساحتها)
در این قسمت شما میتوانید ببینید که یک سیاره در مدار گردشش به دور خورشید در مساحتهای مساوی چگونه رفتار میکند و آیا این قانون برای تمامی سیارات منظومهی شمسی درست میباشد یا خیر.
ابتدا باید یک مساحت دلخواه را تعیین کنید. برای این کار کافی است که در قسمت adjust size مقدار مساحت دلخواه خود را تعیین کنید. مقدار این مساحتی که انتخاب میکنید در زیر این گزینه به صورت کسری و یا به صورت درصدی از مساحت کل بیضی نشان داده خواهد شد.(a fractional sweep size of) و یا به صورت کسری از سال زمین (corresponds to sweep duration of) و یا بر حسب واحد نجومی (and a sweep area of).
وقتی که دکمهی start sweeping را میزنید بر روی شکل مقدار مساحتی که مشخص کردهاید (با توضیحاتی که در بالا دادهام) را به صورت رنگی برای شما نمایش میدهد. اگر گزینهی sweep continuously را انتخاب کرده باشید با فشار دادن این دکمه، شبیهساز ما کل مساحت بیضی را به مساحتهای مساوی تقسیم میکند. که مقدار این مساحتهای مساوی بستگی به شما دارد و شما مقدار آن را با استفاده از گزینههایی که توضیحشان را دادم تعیین میکند.
حال که بیضی را به مساحتهای مساوی تقسیم کردید زمان آن است که به بررسی قانون دوم کپلر بپردازید. مشاهده میکنید که هر سیارهای را که انتخاب کنید مساحتهای مساوی را در زمانهای مساوی طی میکند.
اگر میخواهید برای مساحتهای دیگری این قانون را آزمایش کنید ابتدا دکمهی erase sweeps را فشار دهید تا مساحتهایی که قبلاً بر روی شکل مشخص کردهاید پاک شوند و سپس مساحت جدید را بر روی شکل ببنید. و یا میتوانید بدون پاک کردن مساحتهای رنگی بر روی شکل با جا به جا کردن مقدار adjust size اندازهی این قسمتها را بر روی شکل تغییر دهید.
3ـ سومین قانون کپلر را نیز میتوانید در قسمت Kepler`s 3rd مشاهده کنید. قانون سوم کپلر میگوید که : مجذور دورهی دوران هر سیاره حول خورشید، با مکعب فاصلهی متوسط آن سیاره از خورشید متناسب است. (قانون دورههای تناوب) فاصلهی متوسط سیاره تا خورشید را a مینامیم که برابر نیم قطر بزرگ مدار سیاره میباشد. دورهی دوران هر سیاره حول خورشید را نیز با P نمایش میدهیم. دورهی دوران برابر کقدار زمانی است که طول میکشد که یک سیاره یک بار به طور کامل به گرد خورشید بچرخد. پس طبق این قانون خواهیم داشت : 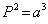 .
.
سیارات مختلف را انتخاب کنید و ببنید آیا این رابطهی برای آنها برقرار است.
در این قسمت یک نمودار داریم که دورهی دوران هر سیاره حول خورشید را بر حسب نیم قطر بزرگ آن نمایش میدهد. با استفاده از این نمودار نیز میتوانید صحت قانون کپلر را مشاهده کنید.
گزینهای در این قسمت داریم با نام plot type که دو حالت linear و logarithmic را میتوانید برای آن انتخاب کنید. این گزینه مربوط به نوع نمایش نمودار میباشد. اگر حالت linear را انتخاب کنید این نمودار را به صورت خطی نشان میدهد و اگر logarithmic را انتخاب کنید این نمودار را به صورت لگاریتمی نمایش میدهد.
میدانیم که در نمایش لگاریتمی فاصلهی واحدهای محورهای مختصات با یکدیگر برابر نمیباشد و به صورت لگاریتمی تغییر میکند ولی در نمایش خطی یک نمودار فاصلهی محورهای مختصات با یکدیگر به یک اندازه میباشد.
4ـ آخرین قسمت این شبیهساز نشان دهندهی سرعت و شتاب سیارات در حرکتشان به دور خورشید میباشد. ابتدا با انتخاب گزینهی Newtonian Features به این قسمت شبیهساز بروید.
در این قسمت نموداری مشاهده میکنید که بر روی آن با خطی آبی رنگ سرعت سیاره را در حرکت به دور خورشید نشان میدهد و با خطی قرمز رنگ شتاب جانب مرکز سیاره را نشان میدهد.
اگر میخواهید سرعت و شتاب سیاره را به صورت برداری بر روی شکل ببینید کافی است که گزینهی show vector را برای v و a انتخاب کنید. در این صورت بردار آبی رنگی که بر روی شکل میبینید بردار سرعت سیاره در حرکت دورانیاش به دور خورشید میباشد و بردار قرمز رنگ بردار شتاب جانب مرکز سیاره در این حرکت میباشد.
در این قسمت میتوانید تغییر سرعت سیاره را مشاهده کنید. میبینید که سیاره هنگامی که در حضیض خورشیدی (کمترین فاصلهی سیاره تا خورشید) میباشد دارای سرعت بیشتری است و در هنگامی که در اوج خورشیدی (بیشترین فاصلهی سیاره با خورشید) سرعتش به کمترین مقدار خود میرسد.
خب تمام قسمتهای این شبیهساز رو برای شما توضیح دادم، حالا شروع به کار شوید و قوانین کپلر را برای تمام سیارات منظومهی شمسی امتحان کنید. ببینید این قوانین در مورد این سیارات درسته یا نه؟ شاید شما تونستید قوانین بهتری برای حرکت سیارات پیدا کنید و اسمتون توی تاریخ نوشته شد. فقط اون وقت یادتون نره که اسمی هم از مدرسهی اینترنتی تبیان ببرید!
نویسنده : علیرضا سرمدی



















